Pavillon rouge et noir

Quand on parle du coût d'une blockchain, on fait souvent référence à son mécanisme de consensus, typiquement de la preuve de travail. Quand on explique que ce coût est exorbitant, il est souvent rétorqué que d'autres mécanismes de consensus à base de preuve d'enjeu peuvent être utilisés et qu'ils sont beaucoup moins consommateur d'énergie. Dans ce billet, je vais m'intéresser au coût d'une blockchain indépendamment du mécanisme de consensus choisi, c'est à dire à une partie incompressible du coût que l'on doit payer quand on choisi d'utiliser une blockchain.

Une blockchain est un registre immuable en ajout seulement (append-only). C'est à dire qu'on ne peut y rajouter de l'information qu'à la suite de ce qui est déjà écrit dedans, et qu'une fois qu'on y a ajouté une information, on ne peut plus modifier ou supprimer cette information. En pratique, cela signifie qu'une blockchain ne contient pas directement l'état d'un système, mais une suite de modifications ordonnées de l'état d'un système. Le sens de cette dernière phrase est probablement assez obscure, je vais donc l'expliquer avant d'en tirer des conclusions.

Commençons avec un exemple qui ressemble^[1] à une cryptomonnaie : le ¢. Dans ce système, il y a des participant·es : Alice, Bob, Charlie, Diane, Emma, et Farid. Initialement il y a deux participant·es qui sont tiré·es au sort et qui reçoivent 5¢ : Bob et Diane. Et donc l'état initial de mon système est que Bob et Diane ont chacun·e 5¢, et que tou·tes les autres ont 0¢. On pourrait noter cet état comme ça par exemple : (A:0, B:5, C:0, D:5, E:0, F:0).

Maintenant faisons tourner notre système. Imaginons que Bob envoie 2¢ à Alice et 1¢ à Farid, et que Diane envoie 1¢ à Bob. On pourrait noter ces transactions comme ceci : [B→A:2, B→F:1, D→B:1]. Le nouvel état du système serait donc (A:2, B:3, C:0, D:4, E:0, F:1). Continuons avec Alice qui envoie 1¢ à Charlie, Bob qui envoie 2¢ à Farid, et Diane qui envoie 1¢ à Emma et 1¢ à Alice : [A→C:1, B→F:2, D→E:1, D→A:1]. Le nouvel état du système serait alors (A:2, B:1, C:1, D:2, E:1, F:3).

Si maintenant je vous pose des questions comme : "Combien Alice possède-t-elle de ¢ ?" ou "Est-ce que Bob peut dépenser 3¢ sans être à découvert ?", vous allez naturellement regarder la dernière version de l'état du système pour pouvoir y répondre directement. Mais, comme je le disais plus haut, si vous utilisez une blockchain, vous n'avez pas un accès direct à l'état du système, mais seulement aux modifications successives de celui-ci. Dans notre exemple, la blockchain ressemblerait à ça :

[_→B:5, _→D:5] ⇒ [B→A:2, B→F:1, D→B:1] ⇒ [A→C:1, B→F:2, D→E:1, D→A:1]

Si vous ne disposez que de la blockchain, pour chaque question vous devez forcément recalculer la partie de l'état du système qui est nécessaire pour y répondre, et cela vous demande forcément de reparcourir toute la chaîne et depuis le début, parce que vous ne pouvez pas savoir à l'avance dans quels blocs il y aura des informations pertinentes. De plus, pour trouver les informations pertinentes, il faut également parcourir l'ensemble des transactions dans chaque bloc pour être sûr de ne pas en rater une où la personne concernée par la question est émettrice ou destinataire.

Sur notre tout petit exemple ça reste raisonnable, mais dans le cas d'un système grandeur nature, où des participant·es peuvent se rajouter au système n'importe quand, où il y a beaucoup plus de transactions dans chaque bloc, et surtout, beaucoup et de plus en plus de blocs, il est impossible de se satisfaire de cette méthode. Ce serait bien trop lent et inefficace.

Pour calculer le coût il faut regarder combien d'opérations doivent être effectuée pour répondre à une question. Ici, une "opération" peut être : suivre un lien dans la chaîne (passer au bloc suivant), lire une transaction (à l'intérieur d'un bloc), faire une addition (quand on voit une transaction entrante pour le compte qui nous intéresse), ou faire une soustraction (quand on voit une transaction sortante pour le compte qui nous intéresse).

Pour répondre à la question "Combien Alice possède-t-elle de ¢ ?" on initialise un compteur (qui représentera le solde de Alice) à zéro, on se place sur le premier bloc, puis on doit faire 14 opérations (je vous laisse les retrouver en vous aidant du dessin ci-dessus) pour pouvoir répondre : "Alice possède 2¢".

Pour répondre à la question "Est-ce que Bob peut dépenser 3¢ sans être à découvert ?", on initialise un compteur à zéro (le solde de Bob), on se place sur le premier bloc, puis on doit faire 16 opérations puis une soustraction pour pouvoir répondre : "non" (de même, je vous laisse faire l'exercice).

Le problème, c'est qu'on doit tout recalculer à chaque fois, et qu'on est obligé de faire des opérations inutiles parce qu'on ne peut pas savoir avant de lire une transaction si elle concerne le compte qui nous intéresse, par exemple. Et bien sûr c'est de plus en plus coûteux à chaque fois que la chaîne grandit par l'ajout d'un bloc.

La solution n'est pas compliquée : idéalement, on ne veut faire qu'une seule fois chaque opération, et se rappeler du résultat pour les prochaines fois. C'est à dire maintenir l'état qui nous intéresse effectivement : le solde de chaque compte. On peut faire ça dans un tableau. Ça ne prend qu'une seule opération d'accéder à une case d'un tableau, et ensuite il suffit de lire le contenu de la case (tout comme on devait lire les transactions)

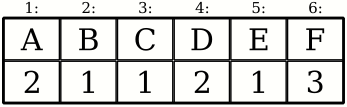
Ici la réponse est récupérée en temps constant : deux opérations (accès à la bonne case du tableau puis lecture de la case), même quand on aura rajouté des nouveaux blocs. Il suffit de maintenir le tableau à jour à l'arrivée de chaque nouveau bloc, une fois pour toutes.

Bon, en pratique, on va plutôt utiliser un logiciel de base de données plutôt qu'un simple tableau, mais l'idée est globalement la même, le coût de l'accès et de la mise à jour de l'information restera très faible (s'il n'est pas constant, il sera logarithmique — comprendre très petit par rapport au nombre d'informations qu'on doit stocker pour représenter l'état du système, et en tout cas toujours indépendant de la taille de la chaîne qui peut donc grossir sans affecter le temps d'accès à l'état du système ou de sa mise à jour). Ce qu'il faut retenir de tout ça c'est que quand on fait le choix d'utiliser une blockchain, ce n'est pas à la place d'une base de donnée "classique", mais bien en plus.

Bien sûr, si on a besoin des fonctionnalités de la blockchain, son coût peut être justifié. Mais le fait est que l'écrasante majorité des projets qui utilisent cette technologie le font sans que ce soit nécessaire, par pur effet de mode. Et dans ces cas là, il est important de comprendre que le coût d'une blockchain (que ce soit celui de son stockage qui ne peut qu'augmenter, ou celui de sa mise en œuvre et de son utilisation comme on l'a vu dans ce billet), aussi petit qu'il soit, est un coût entièrement supplémentaire, puisque pour des raisons pratiques, on doit de toutes façons maintenir également la base de données qui, dans bien des cas, pourrait être utilisée à la place. Et comme une blockchain repose sur un système décentralisé, ce coût supplémentaire est dupliqué chez chaque participant·e !